最終更新日:2014.4.26
このページは前回「逆と裏と対偶」を読んでいる前提で書いています。
引き続き、論理の欠陥(前提と結論のつながり方のミス)について解説します。今回は「必要条件」と「十分条件」について解説します。
『AならばBである』が真実のとき、
『A』を十分条件、
『B』を必要条件、
と呼びます。
『A』であるためには少なくとも『B』である必要があります。
『B』であるためには『A』であれば十分であるといえます。
これは、『A』を『ペンギン』に、
『B』を『鳥』に置き換えて考えてみれば解りやすいでしょう。
『ペンギンならば鳥である』が真実のとき、
『ペンギンであるためには少なくとも鳥である必要がある』、
そして、『鳥であるためにはペンギンであれば十分である』といえます。
このとき、『ペンギン』が十分条件、『鳥』が必要条件にあたります。
◇十分条件について
あるものが鳥であることを証明したいとき、それが『ペンギン』であることを証明すれば、それが『鳥』であることを証明するための十分な証拠になります。(ペンギンならば鳥だから) このとき、『ペンギン』であることは『鳥』であるための十分条件であるといえます。
このように、ある物事が成り立つために十分な条件を、『十分条件』といいます。
◇必要条件について
『鳥』であることは『ペンギン』であるための必要条件です。あるものが『ペンギン』であることを証明したいとき、それが『鳥』であることを証明するだけでは証拠としては不十分です。『ペンギン』であるためには少なくとも『鳥』である必要はありますが、『鳥』にはペンギンだけではなくカラスやツバメもいるからです。
「ペンギンならば鳥である」が真実のとき、
「鳥でないならペンギンではない(対偶)」ので、少なくとも『鳥』である必要があります。
しかし、「鳥ならばペンギンである(逆)」とは限らないので、『鳥』であることを証明しただけでは、それが『ペンギン』であることを証明する根拠としては不十分なのです。
このように、ある物事が成り立つためには必要だけど十分とは限らない条件を、『必要条件』といいます。
◇必要条件とは、ある物事が成り立つために必要な条件を指します。
◇十分条件とは、ある物事が成り立つために十分な条件を指します。
クイズ
前提1.ツバメは鳥である。
前提2.カラスは鳥である。
前提3.ペンギンは鳥である。
以上を図に表したものが以下です。
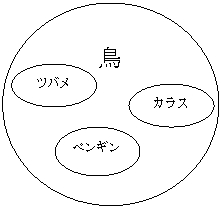
『鳥であるための十分条件は(例えば)ツバメであること。』
『カラスであるための必要条件は 鳥 であること。』
(答えはドラッグすると出ます)
さらにここで前回習った「逆・裏・対偶」を次の文に適用してみましょう。
「カラスならば鳥である」
逆「鳥ならばカラスである」
裏「カラスでないなら鳥でない」
対偶「鳥でないならカラスでない」
さて、図を見てください。
この場合の「逆」と「裏」は必要条件と十分条件を取り違えている
ということが分かりますね。
クイズ 『四枚のカード』
ここに四枚のカードがあります。
「I」 「5」 「J」 「4」
どのカードも、片面にはアルファベット、もう片面には数字が書かれています。
このカードには「片面に母音(A,E,I,O,U)が書かれていれば、もう片面には偶数が書かれている」というルールがあります。
このルールが正しいことを証明するためには、四枚のうち、最低どのカードを裏返せば良い? (裏返す必要のないカードを裏返してはいけません。)
この問題の一般の正答率は数%であると言われています。したがって、もし正解できたなら、あなたはそのたった数%のうちの一人です。なおこの問題は前回記事「逆と裏と対偶」を読んでる前提で出題しています。
ヒント (このカードには四種類の組み合わせがあります。
1.『片面が母音で、もう片面が偶数』のカード。
2.『片面が母音で、もう片面が奇数』のカード。
3.『片面が子音で、もう片面が偶数』のカード。
4.『片面が子音で、もう片面が奇数』のカード。)
ヒント (
カードのルールは『片面が母音なら、もう片面は偶数』でした。
ルールの対偶は『片面が偶数でないなら、もう片面は母音ではない』です。)
ヒント (これは言い換えれば『片面が奇数なら、もう片面は子音である』という意味です。)
ヒント (ゆえに、ルール違反になる組み合わせは
2の『片面が母音で、もう片面が奇数』だけになります。
さて、どれを裏返せば良い?)
超ヒント (それぞれ次のものに置き換えると簡単に解ります。
「母音→子供」、「子音→大人」、「偶数→ジュース」、「奇数→ビール」
ルールは「片面が子供ならば、もう片面はジュースである」です。
(子供はビール飲んじゃダメってこと))
超ヒント (ルールの対偶は
「片面がジュースでないならば、もう片面は子供ではない」です。)
超ヒント (これは言い換えれば『片面がビールなら、もう片面は大人である』という意味です。)
超ヒント (ゆえに、ルール違反になる組み合わせは
2の『片面が子供で、もう片面がビール』だけになります。
カードの四種類の組み合わせ
1.『片面が子供で、もう片面がジュース』のカード。
2.『片面が子供で、もう片面がビール』のカード。←ルール違反
3.『片面が大人で、もう片面がジュース』のカード。
4.『片面が大人で、もう片面がビール』のカード。
さて、どれを裏返せばいい?)
答え: (
「I」.母音の裏は偶数でなければならないので、裏返して確かめる必要があります。
「5」.奇数の裏は母音であってはならないので、裏返して確かめる必要があります。
「J」.子音の裏は奇数でも偶数でもかまわないので、裏返す必要はありません。
「4」.偶数の裏は母音でも子音でもかまわないので、裏返す必要はありません。
◇次のように考えてみてもわかるでしょう。
片面が母音であることは、もう片面が偶数であることの十分条件である。
片面が偶数であることは、もう片面が母音であることの必要条件である。
前提として数字は奇数か偶数のどちらか一方のみである。
ゆえに、
1.表(見えている面)が偶数なら、裏は母音と子音のどちらでも良い。
2.表が母音なら、裏は偶数でなければならない。(奇数ではならない)
3.表が奇数なら、裏は子音でなければならない。(子音でないと十分条件に反する)
4.表が子音なら、裏は奇数と偶数のどちらでも良い。)
◇実際の議論では、複数の必要条件が結合して十分条件として扱われることがあります。次はその例です。
| A氏 「医学部に入るためには、お金だけあれば充分だ」 B氏 「医学部に入るためには、成績も良くないといけないから、お金は必要条件であって、十分条件ではないよ」 |
この場合、B氏は「お金」は「医学部に入る」ためには必要なものだけど、 「お金」だけでは「医学部に入る」ためには十分ではない、という意味で使っています。
(必要条件「お金」+必要条件「良い成績」) → 「医学部に入れる十分条件」
十分条件と必要条件は様々な場面に応用できるので、考えに行き詰ったら思い出してください。
関連サイト
詭弁術の考察―論理間違い
次のページ
前のページ
■HOMEへ 論理的な反論の仕方−クリティカル・シンキング
■TOPへ 論理的思考力と議論とディベート
サブメニュー
【論理的思考法の基礎知識】
クリティカル・シンキング(批判的思考)&えんえき法・きのう法
【前提の正しさを疑う反論】(論証型の反論)
隠れた前提には5つの種類がある
「言葉の定義」の補足
前提(根拠やメリット)に反論する
個々の前提に質問・反論する
「なぜ?」の習慣 批判的思考と質問
【新たな前提を加える反論】(主張型の反論)
想定外の前提&メリット・デメリット比較
【推論の形式(前提と結論のつながり方)を疑う反論】
逆・裏・対偶
論理の飛躍&自己矛盾
【メンタルの管理】
ヒートアップしない、意見と人格を分ける、都合の良い意見も疑う
論理的な反論の仕方についてさらに深く学習したい方には、小野田博一氏の『論理的に話す方法』をお薦めします。論理の欠陥を見つける手法が、やさしい文章で詳しく解説されています。
お客様がこのサイトを採点してください。
アンケートにコメントして頂けると、今後の改善により役立ちます。
(どの項目についての評価かなど)
ご意見、ご感想用の掲示板はこちらです。