


当サイトが最も参考にさせて頂いている
小野田博一先生の新刊が出版されます!
『話す・聞く・考える 「論理力の基本」トレーニングブック』
7月31日発売。予約受付中!
【論理的思考力と議論】
【上級者の実戦を観察する】
【心理と対話】
【その他】
【推論形式の誤謬】
【前提の誤謬】
【レトリック】(暗示にかける表現)
我が社は平均年俸700万円!だからうちに来れば高収入!【統計の誤謬】
最終更新日:2016.1.3
今日は
・統計の誤謬
これをやるぜ!
統計の誤謬
主張の裏付けとして統計資料を引用するのは正しい方法ですが、中には誤った統計データもあります。なお今回は統計学ガチ勢は生暖かい目で見守ってください。
【比較対象の定義が異なる】
「平成11年の交通事故死者数は10300人なんであります。ところが平成12年には9200人に激減しとるんでありますこれ!」
ウソでござる。平成11年度の死者数の定義は「事故後30日以内に死亡した者の数」です。ところが平成12年度の死者数の定義は「事故後24時間以内に死亡した者の数」に変わっています。
このように、同じ言葉なのに定義の違うものを比較する事で、数字を良く見せることができます。
「社会実情データ図録」様から引用したグラフがこちらです。(クリックで拡大)
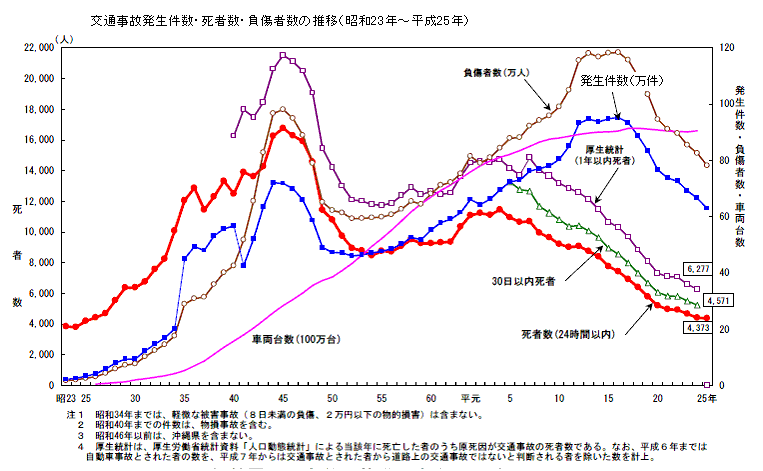
緑の線と赤の線、だいぶ違いますね。
その他にも例えば、失業率は各国で定義が異なるから単純な国際比較はできないという話をよく聞きます。
【偏りのある標本】
統計をとるためには調査したい集団全体(母集団)から、実際に調査する標本(サンプル)を抽出する必要があります。
例えば東京都民の統計をとるために都民全員を調べるのは無理ですから、2千人くらいの都民を無作為に抽出して調べる必要があります。無作為に選ばれた標本の集団は全体の集団とほぼ同じ性質を持ちます。
もし標本が作為的に抽出された場合、統計の信用は失われます。なぜなら偏った標本からは偏った結果が生まれるからです。
例えば「ポルノ雑誌の出版を規制すべきか否か」というアンケート調査をポルノ雑誌の紙面で行えば、結果は「規制に反対」の側に大きくに偏るはずです。なぜなら、そのアンケートの回答者は全てポルノ雑誌の読者だからです。
そのアンケートの回答者は作為的に抽出されており、全体の性質を正しく反映していません。
「インターネット利用に関するアンケートで、インターネットの利用率が100%となっていたことが明らかになった。今年四月にインターネット上でアンケートを実施し、約二万三千人から回答を得た」
ネット利用者しか答えられない。
・次はアンケートの回答率が結果の偏りを生む例です。
ダレル・ハフ著「統計でウソをつく法」から要約して引用します。
ある大学が自校の卒業生の所得を調べるため、卒業生に質問紙を送った。回答率は10%。質問の結果、卒業生の所得は国民平均よりも高い事が判った。
しかし、この結果には偏りがある。なぜなら、貧乏人は高所得者に比べて、所得の公開を嫌がるため、回答率が低いからである。しかも、住所不定の野宿者には質問紙を送る事もできない。したがって、平均を引き下げる人々は、始めから集計の対象から除外されているのである。
問題、「統計でウソをつく法」より引用。
「米西戦争の間、海軍の死亡率は1000人につき9人だった。一方、同期間のニューヨーク市の死亡率は1000人につき16人だった。海軍はこの数字を使って海軍に入ったほうが安全だと宣伝した」
トリックのタネ:(海軍の部隊は健康な青年達から構成されている。一方ニューヨークには赤ん坊、老人、病人もいるから。)
偏りのある標本を使えば簡単に優れた人種や民族を作り出せます。まず民族Aの中から高度な教育を受けた標本(被験者)を集めて、民族Bからは教育を受けていない標本を集めます。それで筆記試験でも受けさせれば民族Aのほうが優れているというウソの証明ができます。
【誘導的な質問】
■質問の仕方で誘導する方法
Wikipedia「統計」より引用。
質問の仕方一つで結果がガラリと変わってしまう。強姦に関するある調査で、女子大生に「男性からアルコールや薬物を飲まされて、望まない性交をした事がありますか」と質問する事で「女子大生の1/4が強姦された事がある」という結論を出したが、批判者達はこの調査で強姦体験者と認定された女子大生達を集めて再調査したところ、その3/4がその体験を強姦だと考えてない事が分かった。
■結果発表の仕方で騙す方法
例えば国民の過半数が靖国神社参拝に反対しているかのようなアンケート結果を作る方法。
まず次のように質問します。
【質問の内容】
靖国参拝についてどう考えますか?
【選択肢】
1.賛成 2.どちらとも言えない 3.反対
アンケート結果が次のようなものだったとします。
【1.賛成】 40%
【2.どちらとも言えない】 30%
【3.反対】 30%
しかし、次のような結果発表の仕方で、事実をごまかします。
1靖国参拝に賛成 40%
2靖国参拝に賛成できない 60%
「賛成できない」の方には「どちらとも言えない」の人も含まれています。あるいは質問の中身を「靖国参拝に賛成ですか?YESorNO」にする事で、どちらとも言えない人はNOを選ぶしかなくなります。
結果のごまかしを防ぐには、調査時の質問内容と選択肢を開示してもらう必要があります。
【空気を読む回答者】
質問者によって回答者の態度が変わるケースです。ダレル・ハフ著「統計でウソをつく法」より引用。
戦争中のことであるが、米世論研究センターが南部の都市に二つの調査団を出して、500人の黒人に三つの質問をさせたことがある。調査団の一方は白人で、もう一方は黒人で構成された。
質問の一つは「もし日本人がアメリカを占領したら、黒人に対する差別は今より少なくなると思うかどうか?」というものであった。黒人の調査団は、質問したうちの9%の人達が少なくなると答えたと報告しているが、白人の調査団によるとそういう答えはたったの2%であった。
また、現在よりも差別がひどくなるだろうと答えた黒人が、黒人の調査団では25%あったが、白人の調査団によると45%になっていた。"日本人"のかわりに"ナチ"とした質問の結果も同じようなものであった。
三番目の質問は、前の二つの質問にあらわれた感情に根ざしていると思われる態度に探りを入れている。すなわち、「日独伊の枢軸国をやっつけるのに全力を集中するのと、国内で、もっと民主主義制度を徹底させるのと、どちらがより重要だと思うか?」この質問に対して、"枢軸国打倒"と答えたのは、黒人調査団によると39%で、白人調査団によると62%であった。
戦時中という特殊な条件下ですが、この実験で回答者が質問者の喜ぶ答えを選んでいることが分かります。
またハフ氏は、街頭調査員は"感じのよさそうな通行人"の所へ質問しに行く傾向があるとも指摘しています。つまり標本が偏るわけです。
【見栄を張る回答者】
回答者のモラルを問う類の質問、例えば「あなたは一日平均、何回歯を磨きますか?」というような質問には、回答者は正直に答えない傾向があります。
また暗数についても考慮する必要があります。
Wikipedia「統計学」より引用。
暗数とは「統計に出ない値」のことで、例えば強姦のような犯罪はそれがタブーであるがゆえに警察に届けないことも多く、したがって統計に表れない。
それには統計を正しく読み解くには暗数を考慮する必要があるが、統計値を多く見積もりたい人は意識的・無意識的に暗数を多く見積もってしまう可能性があり、逆に統計値を少なく見積もりたい人は暗数を少なく見積もってしまう可能性がある。
Wikipedia「暗数」より引用。
1 犯罪を警察に報告されない理由
・一個人が些細なものだとして考えている。
・被害者が捜索されることが厄介で恥ずかしいもの(例:性犯罪)だと感じ、報告しない。
・自分が被害者であると認識していない場合。(例えば、詐欺にかかっている。スーパーで商品が盗まれているのに、それに気づいていない。)
・警察に対する不信感がある場合。
・報告することでの報復や被害のおそれがある場合。
・被害者が加害者(例えば、家庭内暴力や虐待)を害することをしたくない場合。
・子どもが問題だと理解していない場合。(例:動物虐待)
なるほど、おわり。
【利害関係のある調査員】
調査員は完全な第三者であることが望ましいと言えます。なぜなら利害関係者は特定の結果に肩入れをする可能性があるためです。
例えばメーカーが自社製品の性能をテストする実験を行う場合、悪い結果を正直に公表すると利益に悪影響が出るため、都合の良い結果を作り出す可能性があります。
例えばわざと少ない標本数で実験をして偶然の力で都合の良い誤差が出るまで実験を繰り返す方法や、被験者100人で実験をして都合の良い結果が出た20人だけを公表する方法などを使う可能性もあります。
報道番組の街頭インタビューもこれと同じで、制作者にとって都合の良い意見を言っている人だけを選んで映している可能性があります。だいたいは実際にインタビューを行った人数は隠されています。
テレビの科学番組でも、少数の被験者を使って実験を行う場合がほとんどですが、番組の制作費や制作期間が限られている中で、1000人もの標本を集めておき、「やっぱり有意差がありませんでした」というのでは、番組の採算が合わず視聴率も獲得できないはずです。
それならインチキして番組の主要な視聴者層やスポンサーが喜ぶ結果を作り出す可能性もあります。
【視覚で騙す】
グラフをいじって実際よりも良い数字に見せる方法もあります。
これは大阪府の有効求人倍率の推移です。左端のメモリの0.8~1.2だけ間隔が大きくなっているので、棒の長さが実際の数値以上にぎゅ~んと伸びて見えるw
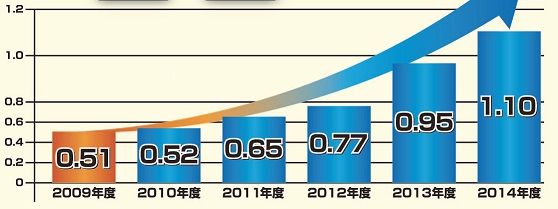
【作為的な解説】
これは児童ポルノの普及が強姦件数を抑制することを説明したグラフです。
「児童ポルノ規制による性犯罪の増加」様より引用させて頂きました。

なるほど、児童ポルノとエロ漫画の規制が強まってから犯罪が増えてる!
これはいかんでござるな!
しかし規制推進派から、上のグラフは規制反対派にとって都合の良い出来事だけを取捨選択しているという批判がつきました。
その証拠に規制推進派に都合の良いグラフも作成可能だとして作られたのがこちら。「児童ポルノ法 ~規制反対派の断末魔が聞こえる~」様より引用させて頂きました。
(クリックで拡大)
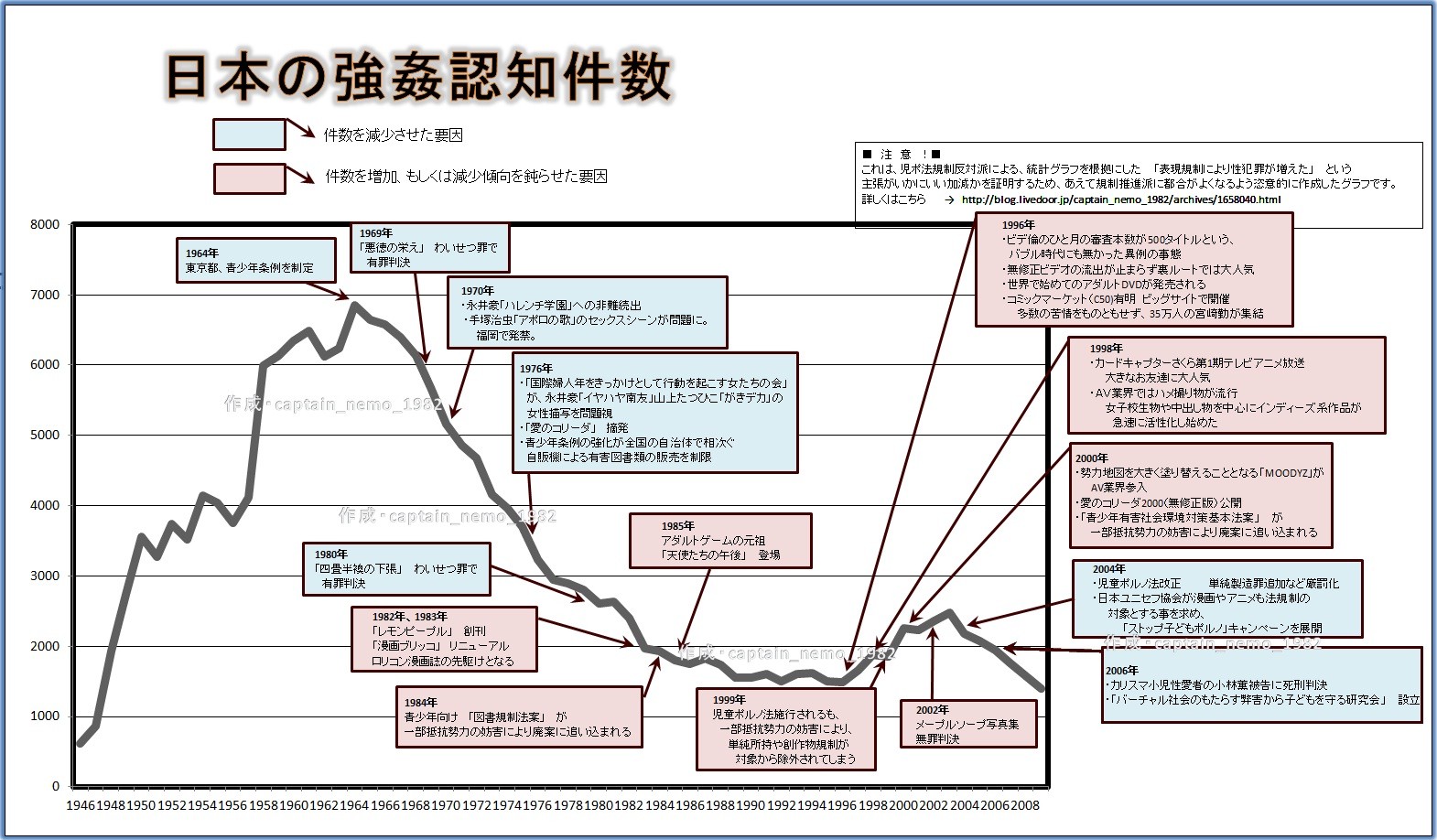
よくぞ見破ったw同じグラフなのに逆のデータに見えるww
作者のnemoさんは、このグラフは意図的な誇張や恣意的表現、データ選択における偏見がふんだんに含まれたネタとして作ったと書いています。(つまり相手も同じことをしていると指摘している)
まあ拙者は初めから信じてござらんかったが・・・・ゲフッゲフッ
要するに確証バイアスで自分の主張に都合の良い出来事ばかり集めていないか、あげた出来事が本当に、またどの程度、統計に影響しているのか、擬似相関ではないかなどに注意する必要があるということですね。
【3種類の平均】
統計上の平均に3つの種類があります。それぞれ、平均値(算術平均)・中央値・最頻値と呼ばれていて、それぞれに特徴があります。
■1.平均値(算術平均)
一般的に平均値と言えばこの算術平均のことです。算術平均では全ての標本の数値を合計して標本の数で割った数字を出します。
例えば、10世帯の平均所得を調べる場合、5世帯の所得が400万円で、ほかの5世帯の所得が500万円なら、合計4500万円÷10世帯なので、全世帯の平均所得は450万円になります。
(単位:一万円)
| A | B | C | D | E | F | G | H | I | J | 平均値 | |
| 所得 | 400 | 400 | 400 | 400 | 400 | 500 | 500 | 500 | 500 | 500 | 450 |
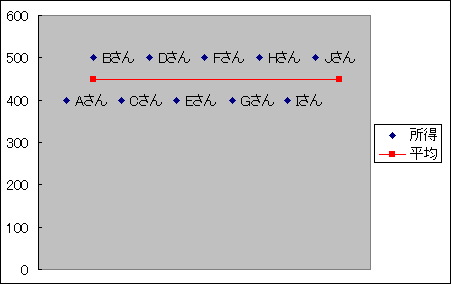
算術平均では全体の分布が分かりにくい点に注意する必要があります。例えば、10世帯中9世帯の所得が200万円で、残り1世帯の所得が2700万円の場合でも、平均所得は450万円になります。下がその図です。
(単位:一万円)
| A | B | C | D | E | F | G | H | I | J | 平均値 | |
| 所得 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 2700 | 450 |
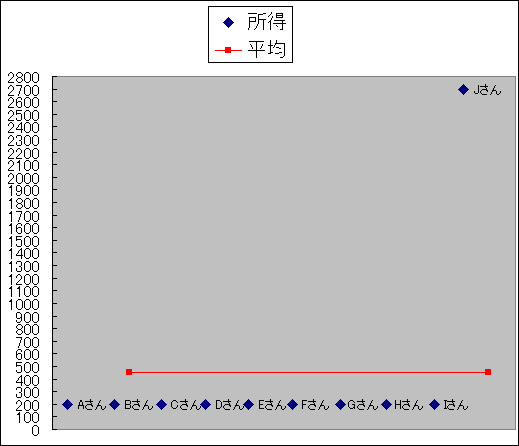
このケースでは一つの世帯が平均を大きく吊り上げています。9世帯が200万円で生活していても、算術平均にすると平均所得は450万円となり、下位90%の所得の2.25倍に達します。
他の例えでは、100人が算数のテストを受けて、うち90人が90点をとり、10人が100点をとった場合、算術平均点は91点なので90人は平均点以下になります。まじです
算術平均値 = 全標本の和÷標本数
■2.中央値
中央値とは全ての標本を数値が大きい順番に並べて、ちょうど真ん中の順位の標本の数値を指します。標本数が偶数の場合は、真ん中に最も近い二つの標本の数値を足して、二で割った数値が中央値になります。
中央値は算術平均よりも実情をよく表している数値だと言えます。次の7世帯の所得の中央値は300万円です。
(単位:一万円)
| A | B | C | G | E | F | G | 平均値 | 中央値 | |
| 所得 | 200 | 230 | 270 | 300 | 500 | 800 | 1200 | 500 | 300 |
(単位:一万円)
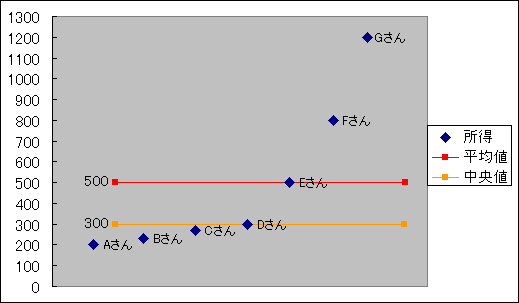
ちょうど真ん中の順位のDさんの所得が中央値になります。つまり、Dさん以外の世帯の半数は中央値よりも所得が高く、もう半数は中央値よりも所得が低いということがわかります。
他の例えでは、101人が算数のテストを受けて、51番目に高い点数をとった人が70点なら中央値は70点です。中央値の上に50人、下に50人いることになります。
■3.最頻値
最頻値とは、数値を一定の範囲ごとに階級分けしたときに、最も多くの標本が集中する階級を指します。
例えば所得の分布が下の図のようになっているとき、所得を100万円単位で階級分けすると、最も多くの標本が集中する階級は300万円以上400万円未満の階級なのでこの階級が最頻値になります。
(単位:一万円)
| A | B | C | D | E | F | G | H | 平均値 | 最頻値 | |
| 所得 | 200 | 300 | 300 | 300 | 300 | 600 | 600 | 1200 | 475 | 300~400未満 |
(単位:一万円)
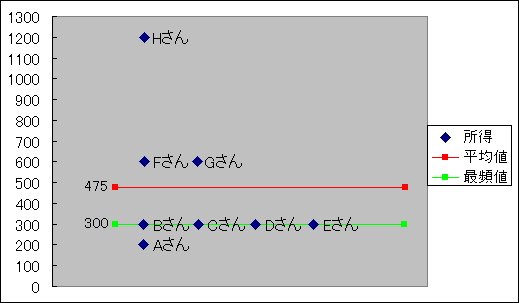
・200万円~300万円 1人
・300万円~400万円 4人 ←最も多い階級
・600万円~700万円 2人
・1200万円~1300万円 1人
300万~400万円未満の所得で生活する世帯が最も多いことがわかります。最頻値はより大多数の実感に近い数値だと言えます。
実例
次は実際のデータを使って算術平均・中央値・最頻値の違いを見てみましょう。
次のグラフは日本人の年収の分布です。
「年収階層分布図2014-年収ラボ」様より引用しました。
(一次資料は国税庁「民間給与実態統計調査」)
横軸が年収、縦軸が人口
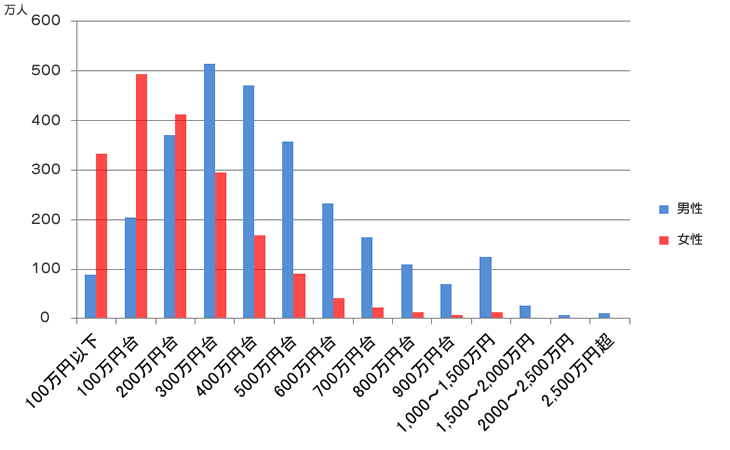
男性に限ると
算術平均値 → 500万円台 (俺のおおざっぱ計算)
中央値 → 400万円台
最頻値 → 300万円台
こんなに差がある。
ついでに言うと男性の収入は50代前半が頂点なので若年層はもっと少ないです。
次は日本人の貯金額の統計です。
総務省統計局 家計調査報告(貯蓄・負債編)-平成26年より引用。
(クリックで拡大)
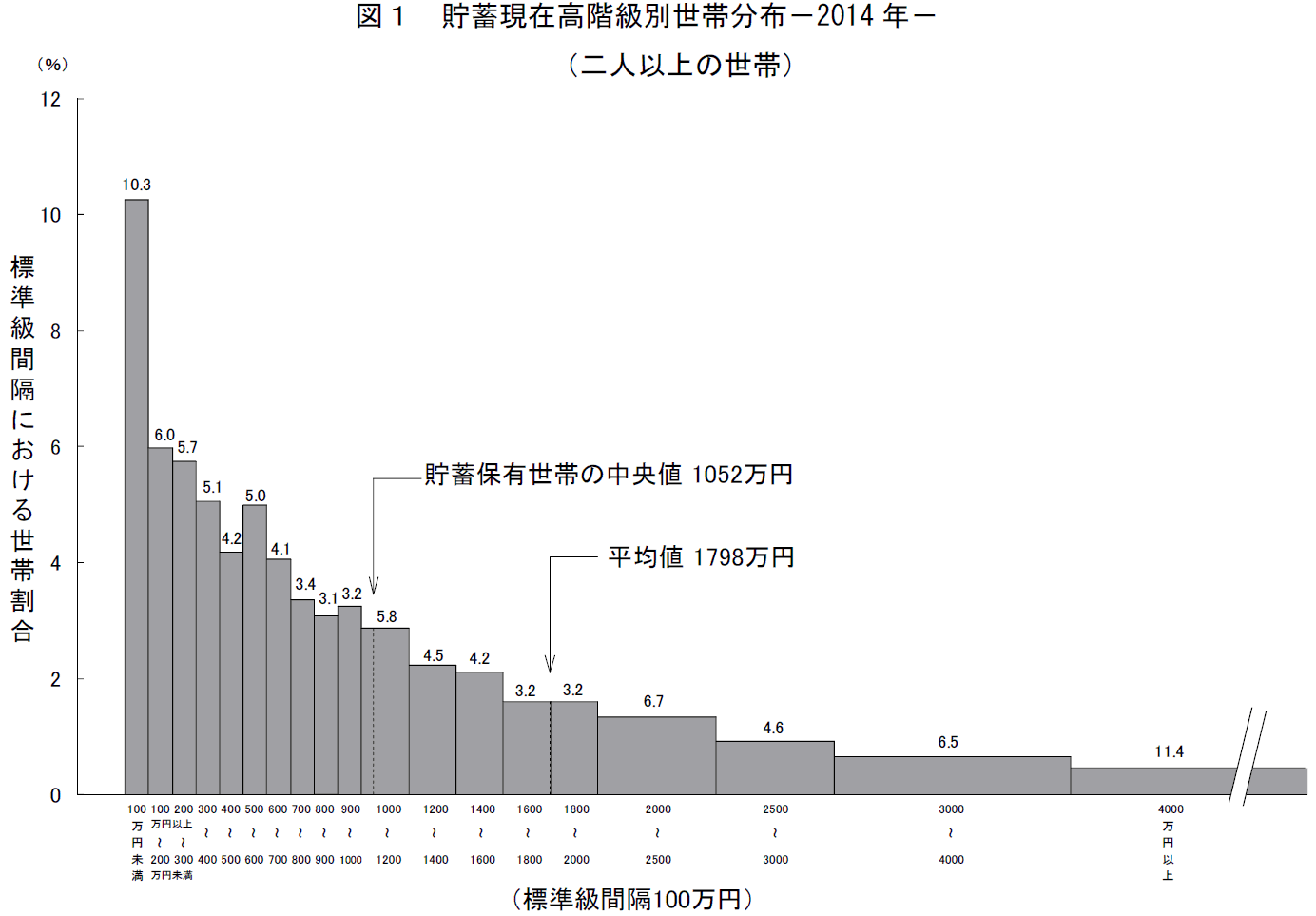
算術平均値 → 1798万円
中央値 → 1052万円
最頻値 → 100万円未満
国民総中流階級!!
【まとめ】
みんな!オラにちっとつ元気を分けてくれ!Tweet
関連サイト(統計)
詭弁術の考察―統計の利用2
暗数 - Wikipedia
統計学 - Wikipedia
中央値 - Wikipedia
最頻値 - Wikipedia
グラフで比較するとそれほど差はないのガイドライン9
関連サイト(テレビ)
マスコミの嘘と裏>関西テレビの歯切れが悪いもうひとつの理由
マスコミの嘘と裏>「からくりテレビ」のからくりとTVやらせ事情
マスコミの嘘と裏>マスコミが絶対批判できない最大のタブーとは?
マスコミの嘘と裏>あるある大辞典(大事典)のニセ実験と洗脳!
教養ドキュメントファンクラブ>回復!スパスパ人間学
教養ドキュメントファンクラブ>発掘!あるある大事典
第3章 詭弁!誤謬!レトリック!―サブメニュー
【推論形式の誤謬】
【前提の誤謬】
【レトリック】(暗示にかける表現)